|
|
… одетый только в халат из холщовой ткани, ходил в кабачки и к певичкам. Когда его спрашивали, почему он таков, он каждый раз открывал рот, засовывал туда кулак и не говорил. Император Лян-цзун призвал его и спросил: «Каков принцип Вашего Пути?» Гуйчжэнь ответил: «Одежда тонка — поэтому люблю вино, выпью вина и защищусь от холода, напишу картину — и расплачусь за вино. Кроме этого, ничего не умею». Лян-цзун не нашелся, что сказать…
От игрушек детства мы движемся к другим. Здесь — об этом.
Алхимия игры включает несколько ингредиентов.
Рецептура состоит из Миров, по которым можно путешествовать; не все из них достаточно хорошо населены. Дело — это Игрушка одного из миров.
Объединяя видимые и сокрытые элементы, Алхимия выступает и как самостоятельный Игрок.
 Передняя панель управляемого стабилизатора тока  Внутренности стабилизатора/источника тока. К задней крышке крепятся, сверху вниз: аналоговая плата, микроконтроллер, бустер. На фронтовой панели органы управления и индикации В моем заказном столе, сразу под столешницей, есть выдвижной ящик. Это промежуточный кэш, куда вначале попадает все что находится на столе, и потом перекочевывает на свои места в другие, менее приоритетные ящики. В последнее время я все время натыкался на свое изделие, а раз так, решил написать про него. Мне нравится, как я сделал аналоговый источник/стабилизатор тока, плюс предмет моей гордости — лаконичный интерфейс состоящий из дисплея на семисегментных индикаторах, крутилка — джойстик на потенциометре и всего две кнопки — Set, Start и Stop.
Аналоговыми вещами я занимался давно, и представился случай тряхнуть стариной — сделать прототип чего-либо подобного.
Даже и не знаю, как его назвать — это разработанный и изготовленный по заказу косметолога приборчик, задача которого — держать выходной ток через внешние электроды стабильным и менять его по определенной программе. Даже и думать не хочу, что планируют делать косметологи со своими пациентами (пытают?), знаю только, что есть много факторов которые будут мешать стабилизации — контакт электродов с кожей, ее потливость (когда пытки становятся интенсивнее), ну и может ее электропроводность, которую никто не может посчитать заранее. Поэтому стабильный ток на выходе — нужен.
Сразу оговорюсь, что я использую термин «ток» не в общеупотребительном смысле, а именно как физическую величину I, в отличие от напряжения U. Напоминаю, что в электротехнике «источник тока» это специальный термин, точно также как и «источник напряжения».
Буду описывать разработанную мной принципиальную электрическую схему пытателя, начиная со второстепенных деталей, и в завершение расскажу подробнее как я сделал собственно сам стабилизатор/источник тока.
 Электрическая принципиальная схема стабилизатора/источника тока На схеме незримо присутствует микроконтроллер (МК) STM32F103, выдавая себя своими контактами. Само собой, на нем крутится программа, на работу которой мы будем иногда отвлекаться.
Начнем с электропитания. Аккумулятор форм-фактора Кроны BT1 подключается через защитный диод Шоттки D1. Не забываем, что косметологи это люди которым ничего не стоит переполюсовать батарею и засадить её против ее контактных площадок. Мы знаем своих клиентов!
Дальше пути 9 вольт расходятся (на самом деле 8.4 В, аккумулятор же, но пусть будет так). Одна линия идет на стабилизатор U1, который питает пищалку (есть и такое) на транзисторе Q1 и ЦАП на транзисторе Q4. Да — да, вы не ослышались, это цифро-аналоговый преобразователь. В нашем простейшем МК его нет, поэтому — сделай сам. К ЦАП мы сейчас вернемся, а пока завершим с электропитанием.
Другая линия 9 В идет на ключ, образованный Q2 и Q3, задача которого — по команде с МК подавать питание на бустер U2, который повышает напряжение до 30 В. Как вы помните, напряжение до 36 В считается относительно безопасным для человеческого организма. Это напряжение используется для формирования стабильного тока.
Вернемся к ЦАП. Его задача — сформировать управляющее напряжение на входе источника тока. ЦАП состоит из операционника U3A (вход 3) и транзистора Q5. Это напряжение будет полностью определять ток во внешней цепи электродов J5. Как работает этот ЦАП? На вход транзистора Q4 подается PWM сигнал от МК. Управление осуществляется изменением скважности PWM, что делает софт — устанавливая ее для заданных временных интервалов или вручную через крутилку. Q4 нагружен на RC цепочку — фильтр нижних частот R5, R6, C1. Постоянная времени фильтра выбрана большой; благодаря этому на выходе фильтра формируется постоянное напряжение, пропорциональное скважности импульсов PWM.
Транзистор Q4 работает в ключевом режиме. Для того чтобы время заряда и разряда конденсатора C1 было одинаковым, используется диод D2: заряд при запертом Q4 идет по цепи 5 В -> R5 -> D2, разряд при открытом Q4 идет по цепи R6 -> Q4. Сопротивления резисторов R5 и R6 равны. Таким образом, цифро-аналоговое преобразование выполняется через управление скважностью цифрового сигнала, с пропорциональным изменением постоянной составляющей которую выделяет RC фильтр.
В схеме есть измеритель выходного тока электродов для его отображения на индикаторе и коррекции. Он реализован на операционнике U3B, выход которого идет на АЦП МК PA1. Выходной ток проходит через токовый шунт номиналом 100 Ом и измерение напряжения (и значит тока) производится на нем.
Потенциометр / крутилка / джойстик подключен к другому АЦП МК PA0, кнопки — к GPIO. Пищалка получает звук от МК и сигнализирует об окончании процедуры. Дисплей подключается по последовательному интерфейсу и работает от МК.
И теперь переходим к главному — собственно к источнику тока. Он реализован на p-n-p транзисторе Q5. Тип p-n-p потому что комфортней иметь общий провод ближе к земле, а не к питанию.
Идея схемы на Q5 — эмиттерный повторитель. Это значит, что благодаря обратной связи по напряжению повторитель держит стабильное напряжение на резисторе в эмиттерной цепи, практически не чувствуя нагрузки (естественно, в определенных пределах). Стабильное напряжение на резисторе — это значит стабильный ток в эмиттерной цепи и соответственно в коллекторной, поскольку это один и тот же ток. Вот так и выглядит дизайн источника/стабилизатора тока.
В статье про однокаскадный усилитель я подробно разбирал принцип действия эмиттерного повторителя. Напомню еще раз — сигнал обратной связи как сигнал рассогласования получается как разность напряжения на базе и падения напряжения на резисторе в эмиттерной цепи. Но в этой схеме я пошел еще дальше. Я дополнил схему операционником, благодаря чему сигнал рассогласования усиливается многократно, что ведет к более стабильной работе схемы. U3a с одной стороны на неинвертирующем входе получает управляющее напряжение, которого он должен держаться, на инвертирующем — сигнал обратной связи с эмиттерного резистора R14. За счет большого усиления в этой цепи, гораздо большего чем может себе позволить одиночный транзистор, номинал резистора R14 можно держать низким, что благоприятно сказывается на диапаоне выходных токов схемы. Будут вопросы по схеме — пишите!
В такого типа устройствах, когда провода выходят наружу, первым делом возникает мысль — а что если их закоротить и тем самым сжечь прибор? Это как раз не наш случай. Режим короткого замыкания для источника тока — самый комфортный и естественный режим. Теоретически, для него разомкнутая цепь также катастрофична как и короткозамкнутая для источника напряжения.
То, про что еще можно рассказать — это софт. Тут вы сами можете дать волю своему творчеству. Со своей стороны замечу, что несмотря на простоту, дисплей имеет хорошую функциональность — на нем можно отображать и выбирать пункты меню, пользуясь крутилкой/потенциометром для скроллинга, задавать этой же крутилкой таймеры и выходной ток, задавать сложные программы когда выходной ток должен меняться со временем.
Пока прототип ушел к своему заказчику, и не исключено что мы его запустим в серию. Но это уже про маркетинг )
Двигаемся поэтапно, с самого начала.
1. Никаких виртуальных функций (пока что)
Используем struct вместо class чтобы каждый раз не писать public. В нашем примере не будет никаких приватных членов класса, а в остальном все тоже самое:
|
|
struct Parent { void f() {} // (1) }; struct Child : public Parent { void f() {} // (2) }; |
Функция f() переопределена в дочернем классе Child (overriding, не путать с overloading). Вызов функций:
|
|
Parent* p = new Parent; p->f(); // будет вызвана (1) Child* p = new Child; p->f(); // будет вызвана (2) |
Пока никаких неожиданностей нет — все работает как должно.
Замечу, что если в дочернем классе не будет функции (2), то будет вызвана функция (1) родительского класса. Это происходит потому, что Child хранит гены родителя Parent и в силу наследования имеет доступ ко всем полям родительского класса. Но это так, к слову.
2. Все еще никаких виртуальных функций
Сделаем странную вещь — присвоим указателю на объект родительского класса объект производного класса и поразмышляем над тем, что получилось.
|
|
Parent* p = new Child; p->f(); // будет вызвана (1) !!! |
Указатель на Parent, а объект Child… нет ли здесь несоответствия или противоречия?
Рассуждаем так. Указатель на объект класса — это не просто адрес в памяти. Когда мы имеем дело с классами, фактически имеем набор указателей на все поля и функции класса — это если упростить (а упрощать мы любим). Выше я говорил, что Child хранит «гены» родителя Parent, в нашем случае — функцию (1) родительского класса. Поэтому указатель на Parent находит в Child то, про что он знает — отсылку на свою собственную функцию (1).
При этом родительский класс не знает абсолютно ничего про остальные поля и функции, которые эксклюзивно находятся в Child. И если последний содержит например функцию g(), то компиляция p->g() даст ошибку.
В ситуации наоборот
|
|
Child* p = new Parent; // ошибка компиляции |
Указатель захочет сослаться на поля, которые есть только в Child, но в объекте Parent их быть не может!
3. Подозрительная конструкция
Поехали дальше. Возникает закономерный вопрос: зачем вообще нужна такая конструкция
когда все прекрасно работает и без нее? Следствие, которое ведут Колобки, знает: встретили такую запись — значит где-то поблизости виртуальная функция (и может быть не одна).
И наоборот — видите объявление виртуальной функции, ищите в коде конструкцию подобного вида: она обязательно будет, потому что без нее объявлять функцию виртуальной нет смысла.
Поэтому смотрим пока на то что «нет смысла», а потом переходим к заключительному полноценному примеру.
4. Бессмысленная виртуальная функция
|
|
struct Parent { virtual void f() {} // (1) }; struct Child : public Parent { void f() override {} // (2) }; |
Теперь функция f() стала виртуальной. Заведите хорошую привычку дописывать override в дочерних классах, чтобы во-первых было понятно что функция виртуальная (это здесь все видно, а если вы копаетесь в многочисленных листингах?), и во-вторых это страхует вас от ошибки в сигнатуре функции — без override компилятор все пропустит, но будет считать f() в дочернем классе уже не виртуальной, а с override — предупредит.
Повторяем наш эксперимент с самого начала.
|
|
Parent* p = new Parent; p->f(); // будет вызвана (1) Child* p = new Child; p->f(); // будет вызвана (2) |
Вы заметили какую — нибудь разницу по сравнению с первым сценарием без виртуальных функций? И я тоже нет.
Давайте быстро забудем про это бессмысленное применение virtual и перейдем к нашей сакраментальной конструкции, и тут она уже заиграет в полную силу.
5. Складываем все вместе
Объявление класса с виртуальными функциями:
|
|
struct Parent { virtual void f() {} // (1) }; struct Child : public Parent { void f() override {} // (2) }; |
Действие:
|
|
Parent* p = new Child; p->f(); // будет вызвана (2) !!! |
У меня для вас новость: объект родительского класса каким-то образом узнал про функцию в дочернем классе и вызвал именно ее. Как он это сделал?
Сейчас самое главное — не погрузиться в дебри новых понятий и не потерять прозрачность повествования. Новое понятие — это таблица виртуальных функций vtable класса Parent, которая содержит указатели на виртуальные функции. Отныне все вызовы виртуальных функций будут происходить не через указатель класса Parent* p, а через посредника — таблицу vtable.
Принципиально важным является то, что содержимое этой таблицы не задается жестко во время компиляции, а может меняться по ходу выполнения программы (это то, что вас на собеседовании спрашивали про позднее связывание или dynamic binding). Если мы поймем, как и когда эта таблица заполняется и меняется, мы поймем все про виртуальные функции. Поехали!
6. Gdb, vtbl
Ехать будем с помощью отладчика gdb — это наиболее удобный способ посмотреть расположение vtable и виртуальных функций в памяти. Поменяем наш пример, чтобы с отладчиком было удобнее работать:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
#include <iostream> using namespace std; class Base { public: virtual void base_and_derived(void) { cout << "Base::f" << endl; } virtual void base(void) { cout << "Base::fonly" << endl; } }; class Derived : public Base { public: void base_and_derived(void) override { cout << "Derived::f" << endl; } virtual void derived(void) { cout << "Derived::v" << endl; } }; int main (int argh, char *argv[]) { Base* b = new Base(); Derived* d = new Derived(); b = d; return 0; } |
Компилируемся, запускаем отладку:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
(gdb) b main Breakpoint 1 at 0x11dd: file faddr.cpp, line 21. (gdb) run Starting program: /home/***/faddr [Thread debugging using libthread_db enabled] Using host libthread_db library "/lib/x86_64-linux-gnu/libthread_db.so.1". Breakpoint 1, main (argh=1, argv=0x7fffffffdfc8) at faddr.cpp:21 21 b = new Base(); (gdb) n 23 d = new Derived(); (gdb) n 24 b = d; (gdb) info vtbl b vtable for 'Base' @ 0x555555557d50 (subobject @ 0x55555556aeb0): [0]: 0x5555555552a0 <Base::base_and_derived()> [1]: 0x5555555552de <Base::base()> (gdb) info vtbl d vtable for 'Derived' @ 0x555555557d28 (subobject @ 0x55555556aed0): [0]: 0x55555555531c <Derived::base_and_derived()> [1]: 0x5555555552de <Base::base()> [2]: 0x55555555535a <Derived::derived()> |
Замечу что b = d еще не выполнялось: мы остановились до этой строчки.
Для успокоения души проверим адреса, которые нам выдал отладчик, например для b:
|
|
(gdb) x /2xg 0x555555557d50 0x555555557d50 <_ZTV4Base+16>: 0x00005555555552a0 0x00005555555552de |
Все в порядке, vtable содержит адреса Base::base_and_derived() и Base::base() (доверяй, но проверяй!)
Теперь посмотрим на таблицы, на какие виртуальные функции они указывают. С классом Base все понятно, это пара собственных виртуальных функций base_and_derived(), base(). С дочерним классом Derived немного интереснее: его таблица содержит переопределенную виртуальную функцию базового класса base_and_derived(), собственно виртуальную функцию base() которая принадлежит базовому классу (родитель!) и собственная виртуальная derived().
Само собой, адреса виртуальных таблиц 0x555555557d50 и 0x555555557d28 различаются, поскольку у каждого класса (не экземпляра класса!) своя виртуальная таблица. Это замечание пригодится нам прямо сейчас.
Продолжаем программу и выполняем наше легендарное присвоение указателя производного класса указателю базового класса:
|
|
(gdb) n 26 return 0; (gdb) info vtbl b vtable for 'Base' @ 0x555555557d28 (subobject @ 0x55555556aed0): [0]: 0x55555555531c <Derived::base_and_derived()> [1]: 0x5555555552de <Base::base()> (gdb) info vtbl d vtable for 'Derived' @ 0x555555557d28 (subobject @ 0x55555556aed0): [0]: 0x55555555531c <Derived::base_and_derived()> [1]: 0x5555555552de <Base::base()> [2]: 0x55555555535a <Derived::derived()> |
Произошли существенные изменения, и главное из них — мы фактически потеряли виртуальную таблицу базового класса (что еще можно было ожидать от присваивания?) Точнее, базовый и производный класс сейчас содержат только одну виртуальную таблицу расположенную по адресу 0x555555557d28, которая по сути таблица класса Derived оставленная без изменений —.
Поскольку класс Base теперь пользуется виртуальной таблицей класса Derived, предыдущая запись
0x5555555552a0 <Base::base_and_derived()>
Поменялась на запись
0x5555555552a0 <Base::base_and_derived()>
какой она и была для Derived раньше.
Это означает: все вызовы виртуальной функции base_and_derived выполненные с помощью указателя b->base_and_derived() приведут не к вызову виртуальной функции базового класса (как можно было ожидать, ведь b — указатель на Base), а к вызову виртуальной функции произвольного класса.
Что и требовалось доказать.
7. Послесловие
Вот и все. Приведу пример, когда это бывает нужно в реальной жизни. Например, клиент знает только про класс Interface и пользуется им:
|
|
struct Interface { virtual int api() {} // client interface }; // то что ниже - клиенту знать не обязательно struct Implementation_1 : public Parent { int api() override {} // api version 1 }; struct Implementation_2 : public Parent { int api() override {} // api version 2 }; |
У нас есть возможность подсовывать различные варианты реализации интерфейса, оставляя клиента в неведении:
|
|
Interface* if; if = new Implementation_1; if->api(); // будет вызвана версия 1 api if = new Implementation_2; if->api(); // будет вызвана версия 2 api |
Этот пример можно воспринимать по другому: например, Implementation_1 это боевая реализация, а Implementation_2 это mock заглушка для тестирования. Или Interface это класс прокси или адаптера. В общем все шаблоны C++ которые только существуют базируются на этой записи:
и это все, что вам нужно знать про полиморфизм в C++.
Понимаю, тема несколько выбивается из ряда… но разнообразие прекрасно, полезно и бодрит, поэтому продолжаем. В последние два с половиной года я был сильно погружен коммерческую разработку на C++ , мой стол набитый комплектацией простаивал без дела, и вот пришло время размяться на аналоговом поле.
На самом деле микрофонный усилитель — это не просто так, а часть моего проекта, который я завершу — когда нибудь, надеюсь. Задача усилителя — завести голос с микрофона гарнитуры на АЦП STM32. Определенное время я развлекался, знакомясь с ужасными схемотехническими решениями, которые кочуют с сайта на сайт (высокоимпедансный микрофон на вход схемы с общим эмиттером), и решил дать простое решение с подробными разъяснениями (фокус с последующим разоблачением).
Итак, смотрим чертеж.
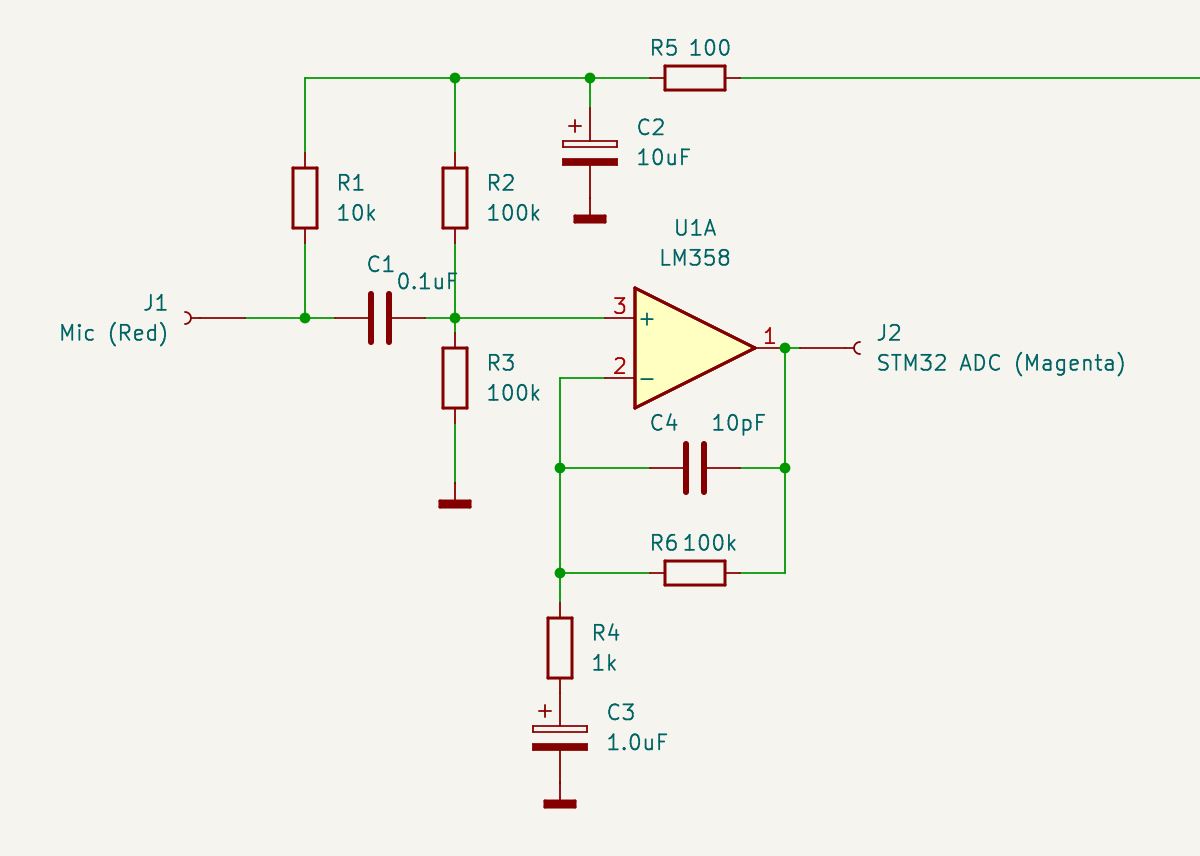 Микрофонный усилитель на LM358 / Microphone amplifier LM358 Слева подключаем микрофон, справа подаем выход усилителя на АЦП микроконтроллера. Пусть обозначения цветов вас не смущают — это маркировка проводов в моем монтаже.
Начинаем с микрофона. В гарнитуре он или электретный, или конденсаторный. И в том и другом случае на него нужно подать питание, что делает резистор R1, обеспечивая положительное смещение. Также и в том и другом случае микрофон имеет высокий импеданс, поэтому нагрузочный каскад должен иметь высокое входное сопротивление. Ходят легенды, что в микрофоны встраивают полевой транзистор, который обеспечивает высокоомную нагрузку для него — благо что питание подавать все равно надо. Я специально разобрал такой один, но транзистор вероятно был настолько мал, что я его не нашел даже под лупой.
Поэтому пусть будет универсальное решение — вход нашего усилителя будет высокоомным, поэтому подаем сигнал с микрофона на (+) вход операционного усилителя — ОУ. И давайте примем, что сопротивление входа (+) ОУ будет бесконечным, поэтому входную нагрузку будут определять параллельно включенные R2 и R3 (да — да, вы не ослышались — для сигнала что питание что земля все едино, поэтому микрофон получает нагрузку 50 кОм).
Лирическое отступление — почему на (+), а не на (-)? Ведь входы ОУ равноценны и образуют дифференциальный транзисторный каскад. Все дело в отрицательной обратной связи через R6, благодаря которой вход (+) становится высокоомным. Как это работает — рассказал на примере эмиттерного повторителя .
Давайте сразу про обратную связь. Она весьма двулична и ведет себя по-разному по постоянному и переменному току. По постоянному току играет R6 (и в этом варианте он вообще не нужен — мы могли бы накоротко замкнуть выход ОУ и вход (-)). Обратная связь получается 100 — процентной, поэтому коэффициент усиления каскада по постоянному току — единица, и средняя точка, которую устанавливает делитель R2/R3, будет такой же на выходе операционника, то есть — половина напряжения питания.
Теперь про обратную связь по переменному току. Здесь играет конденсатор C3, который закорачивает нижний конец резистора R4 на землю, в результате чего в цепи обратной связи появляется делитель R6/R4. Тут уже резистор R6 выполняет свою роль и совместно с R4 устанавливает коэффициент усиления каскада по переменному току, равный 100.
Конденсатор C4 давит усиление на высоких частотах, что лишает широкополосный LM358 возможности самовозбудиться на высоких частотах (вполне реальная перспектива, если фазовый сдвиг в цепи обратной связи получится другим нежели чем 180).
Поскольку режимы по постоянному току для микрофона и входа (+) ОУ — разные, изолируем эти цепи конденсатором C1. Надеюсь, не надо объяснять, что он проницаем для входного сигнала, и неожиданно маленькая емкость — 0.1 мкф совсем не большое препятствие, потому что опять таки — вход высокоомный.
Как вы наверное догадались, линия в верхней части, уходящая вдаль направо — это питание 3.3 В. Столько я рассчитываю получить с USB смартфона (ну вот, проговорился про еще про один кусок будущего проекта).
Для LM358 такое напряжение — нормально. Заметим, что выходной сигнал будет меняться не относительно земли (разделительного конденсатора на выходе ОУ нет), а между землей и 3.3 В — что АЦП и надо.
Для чего нужна цепочка R5C2? Практикующие инженеры знают, что мусор в цепях питания — обычное дело. На чувствительном входе каскада ОУ он нам совсем не нужен, и поэтому фильтр R5C2 будет прибивать все что по частоте выше постоянного тока (в идеале).
Пара электролит — керамика для сброса мусора на землю также стоит в правой части, которая не видна. Зачем керамический конденсатор маленькой емкости в параллель с электролитическим? Последние имеют неприятное свойство — паразитную индуктивность. Поэтому с ростом частоты они будут не очень хорошим конденсатором.
На макетке операционник в левой части. Особо зоркие могут заприметить транзистор в правой части — не обращайте на нее внимание, это очередной кусок проекта (который надо полностью поменять).
В результате экспериментов выяснилось, что усилитель держит неплохую полосу от 100 Гц до 10 кГц и негромких песен вполне достаточно до раскачки выхода от 0.5 В до 2.5 В.
When using numpy at the beginning of a project we don’t think about performance. This is because it is more important for us to get solution that works. And only then, with real data, observing how our computer begins to slow down, we have to find answer on how to avoid this. And then we
Читать дальше
Когда люди начали создавать компьютеры, сравнение с аналогичной продукцией живой природы не заставило себя ждать. Все (за редким исключением) сошлись во мнении, что нейросистемы животных слишком сложны и медленны, чтобы быть достойными более глубокого изучения. Здесь под изучением я подразумеваю не биохимический анализ нейронов, а понимание уровня системы: по каким алгоритмам она работает и самое
Читать дальше
По сравнению с такими шустрыми средствами, как противорадиолокационные ракеты (Anti Radar Missile) беспилотник выглядит сущим недоразумением. Однако, это всего лишь следствие инерции мышления, когда на самом деле главный недостаток БЛА по сравнению с ракетой — низкая скорость, становится преимуществом в следующих случаях:
нужно хорошенько рассмотреть цель; можно позволить себе прогуляться для того чтобы выбрать что-либо
Читать дальше
Множество психотехник проникает в нашу жизнь. Одна из них — визуализация желательных событий. Утверждается, что представляя объект своих устремлений в виде образа — мысленно, или в звуках или хотя бы на бумаге — вы рано или поздно его получите. Наконец найден волшебный эликсир для диванной армии вершителей реальности: не затрачивая времени и сил, сберегая нервы
Читать дальше
В статье маркеры визуальной системы автоматической посадки БЛА была описана обработка видео-данных реального времени для системы оптического типа — VBLS. Это была хоть и шустрая, сделанная на C++, но модель. Теперь, как было замечено в конце этой статьи, пришло время показать систему в боевом варианте, где обработка видеопотока параллелится в ПЛИС.
В данной системе для
Читать дальше
Визуальная автоматическая посадка БЛА может выполняться не только по характерным точкам местности, но и по специально подготовленным и известным изображениям — маркерам. Собственно сама стандартная разметка ВПП состоит из таких маркеров, только исторически они предназначались не для обработки компьютером, а для человека — пилота. Поэтому нет ничего удивительного в том, что искусственный интеллект дрона потребует
Читать дальше
Эта история конечно имеет свои универсальные черты. Это означает, что разработка любой отечественной военной техники, не попадающей под непосредственное внимание первых лиц, идет примерно схожим образом. С другой стороны, в каждом проекте есть свои, отличающиеся от других особенности, и поэтому каждый волен выбирать, как ему воспринять эту историю: еще раз убедиться в том, как она
Читать дальше
|
|
Last comments