При рассмотрении метода главных компонент я не стал подробно останавливаться на том, в чем смысл связи корреляционной функции и линейного преобразования исходных данных. Сейчас пришло время вникнуть в это поподробнее. К тому же этот материал пригодится нам в будущем, когда будем рассматривать такой метод сверхразрешения, как MUSIC.
В изложении я минимизировал формульную часть; там где это необходимо показал формулы в нотации Питона. Поэтому все выкладки которые приведены очень легко проверить буквально в режиме командной строки.
Начнем с формирования исходных данных.
Шум и ничего более
Будем работать с двумя массивами, или как любят говорить в линейной алгебре — векторами. Переменные x0 и x1 будут представлять из себя независимые друг от друга векторы с нормальным распределением со средним 0 и дисперсией равной единице.
Почему переменных будет именно две? Только по той причине, что двумерные распределения удобно смотреть на плоском графике 🙂 Можно конечно работать и с трех- и многомерными переменными, но в этом случае наглядность может пострадать 🙂
В любом случае, этот пример можно распространить на любое количество измерений.
|
1 2 3 4 5 |
import numpy as np x = np.zeros((2,N)) x[0,:] = np.random.normal(0,1,N) x[1,:] = np.random.normal(0,1,N) x = np.mat(x) |
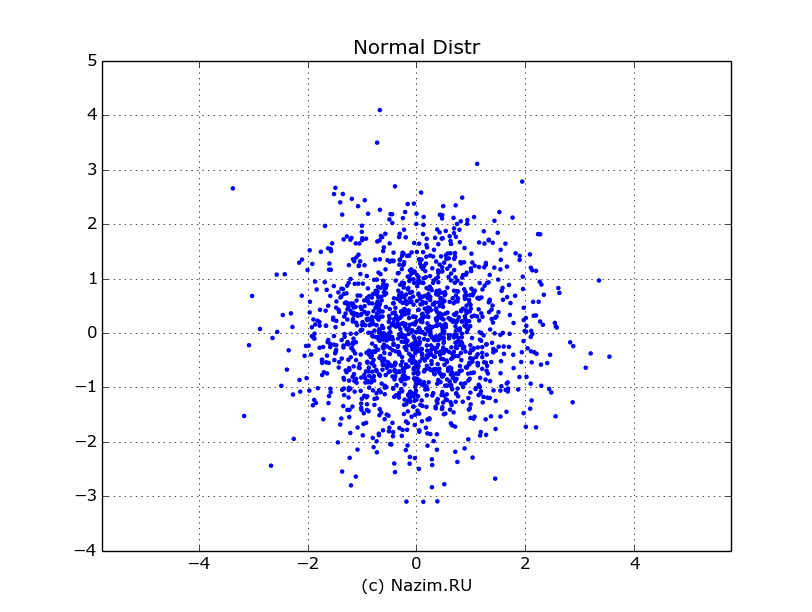
Я сразу сохранил два этих вектора в одной матрице x для удобства дальнейшей работы. Вот что получилось при отрисовке при N=1500 (по оси абсцисс — x0, по оси ординат — x1):
Из графика видно, что наибольшая плотность вероятности действительно лежит в точке (0,0). Переменные независимы друг от друга, потому что точки с координатами (x0,x1) распределены равномерно вокруг центра.
Независимость, или некоррелированность, мы можем подтвердить также путем вычислений:
|
1 2 3 4 |
np.cov(x) [[ 1.011 0.011] [ 0.011 1.016]] |
Единицы ковариационной матрицы по главной оси показывают, что переменные коррелированы сами с собой (другого и не ожидалось), а близкие к нулю значения, показывающие взаимную корреляцию говорят о том что переменные практически не зависят друг от друга.
Сделаем небольшое отступление: почему мы работаем с матрицей ковариации а не корреляции? Исторически сложилось, что корреляцию воспринимают как ковариацию, нормированную в диапазон -1, … +1. Нормировка нам не к чему, поэтому мы работаем с матрицей ковариации.
Теперь, когда мы знаем, с чем имеем дело, пора переходить к следующему шагу: подвергнуть наши векторы линейной трансформации.
Линейное преобразование двух случайных векторов
Трансформацию векторов x0,x1 получают перемножением векторов на матрицу трансформации A, в результате чего получится уже новая пара векторов. Трансформация будет состоять из двух частей: матрицы поворота ROT на угол 20°
|
1 2 3 4 5 6 |
theta = np.pi*20.0/180.0 ROT = np.mat([[np.cos(theta), -np.sin(theta)], [np.sin(theta), np.cos(theta)]]) [[ 0.94 -0.342] [ 0.342 0.94 ]] |
и матрицы масштабирования SCALE с коэффициентом 4 по оси х и коэффициентом 0.5 по оси y:
|
1 |
SCALE = np.mat([[4.0,0],[0,0.5]]) |
В результате матрица трансформации A как произведение только что заданных матриц поворота и масштабирования будет такой:
|
1 2 3 4 |
A = ROT*SCALE [[ 3.759 -0.171] [ 1.368 0.47 ]] |
Ну и в результате получим трансформированные векторы, чего мы и добивались:
|
1 |
xa = A*x |
На рисунке изображение всех значений вектора xa выделено зеленым цветом.
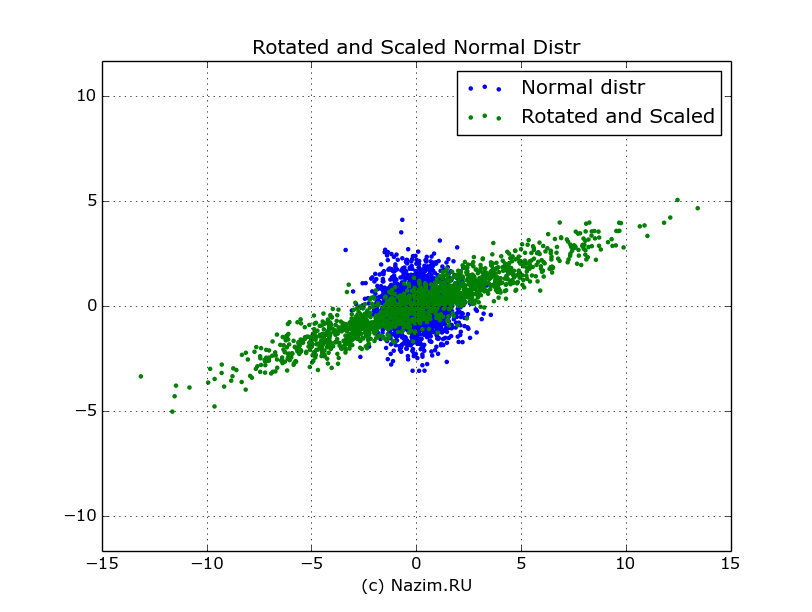
Исходное нормальное распределение (синий цвет) и распределение после его трансформации: поворота и масштабирования (зеленый цвет)
Наше нормальное распределение деформировалось: теперь оно уже далеко не нормальное: вытянулось вдоль одной оси, сжалось вдоль другой и вдобавок еще повернуто. Но самое главное из того что произошло, это то что теперь новые векторы больше не являются независимыми: например, если первый из трансформированных векторов принимает значения >10, то с высокой степенью вероятности второй вектор будет принимать значения >3, как следует из распределения. В исходном распределении такого не было: любому из значений x0 могло соответствовать любое значение x1 из области распределения.
Теперь эту зависимость отражает и ковариационная матрица:
|
1 2 3 4 |
COV = np.cov(xa) [[ 14.301 5.135] [ 5.135 2.131]] |
Значение 5.135 недвусмысленно намекает на взаимосвязь между трансформированными векторами.
Здесь самое время задаться вопросом: поскольку ковариационная матрица является обобщенной характеристикой нового распределения, которое в свою очередь получено в результате трансформации A, существует ли связь между ковариацией и линейной трансформацией A?
Физический смысл ковариационной функции линейного преобразования
Заголовок отражает суть того, до чего мы докапываемся. Интуитивно понятно, что корреляция возникает в процессе изменения вектора, то есть линейной трансформации. Вначале отметим для себя вывод, к которому мы пришли: если подвергнуть линейному преобразованию нормально распределенные векторы, то ковариационная функция такого преобразования будет полностью определяться матрицей линейного преобразования.
Другими словами, все взаимосвязи в результате будут определяться матрицей линейного преобразования.
Можно решить и обратную задачу: если мы хотим получить результат с определенными корреляционными свойствами, можно найти матрицу линейного преобразования над случайным процессом, которое приведет к требуемому результату.
Поскольку мы занялись поисками смыслов, то самое время пристегнуть к нашей парочке ковариационная матрица — матрица линейного преобразования еще и собственные числа и собственные векторы.
В статье посвященной методу главных компонент мы занимались поиском собственных значений матрицы линейного преобразования. А что если найти собственные векторы и числа ковариационной матрицы? Сказано — сделано:
|
1 |
[en,ev]=np.linalg.eig(COV) |
В результате получаем собственные векторы
|
1 2 |
[[ 0.939 -0.343] [ 0.343 0.939]] |
и собственные числа:
|
1 |
[ 16.178 0.254] |
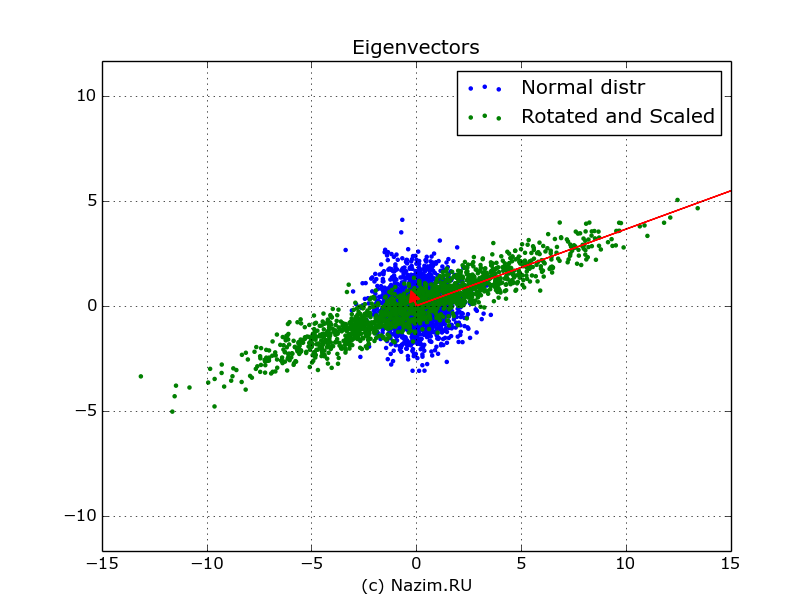
Отрисуем их на нашем распределении красным цветом. При этом само собой масштабируем собственный вектор собственным числом:
Пусть вас не смущает отсутствие стрелочки справа: она как раз находится за полем рисунка.
Собственные векторы ковариационной функции показывают направления линейной трансформации исходного распределения. Это уже второй смысл ковариационной функции нормального распределения.
Далее, собственные векторы можно определить и так: они соответствуют направлению максимальной изменчивости, или вариабельности сигнала.
Теперь, вернемся к матрице линейной трансформации и сравним ее с собственными векторами и числами. Нетрудно заметить, что набор собственных векторов есть не что иное, как матрица поворота ROT, а собственные числа — это значения матрицы масштабирования SCALE в квадрате. Это не случайное совпадение, характерное для нашего примера, а строгое теоретическое соответствие. Тогда круг замыкается: то, каким образом мы трансформируем исходное «белое» распределение, в результирующем сигнале станет собственными векторами и числами его ковариационной матрицы.
Коротко о главном
Подведем итоги. Ковариационная матрица полученных данных непосредственным образом связана с линейной трансформацией исходных некоррелированных данных, сформированных как белый шум с нормальным распределением. В свою очередь, линейная трансформация порождает значения собственных векторов и чисел ковариационной матрицы. В то время когда собственный вектор соответствует матрице вращения, собственные числа соответствуют масштабированию входных данных по каждой из осей.
Есть определенный глубинный смысл в том, что мы в конечном счете работаем только с ковариационной функцией сигнала, не обращая внимания на сами наборы данных, для которых она была получена. Данные могут меняться, но взаимосвязи остаются: ведь в конце концов корреляция в сигналах есть не что иное, как указание на передаточную функцию фильтра, с помощью которого этот сигнал был сформирован из белого шума. Шум изменчив, передаточная функция постоянна. Ковариационной функции достаточно.
Updated 06.05.2018

Ответить