Ортогонализация Грама — Шмидта/Gram — Schmidt в адаптивном фильтре

Разбирая свойства 2D альфа — бета фильтра для траекторной обработки радарных данных, мне постоянно приходилось уходить в сторону ортогонализации входных данных. Поначалу не очень хотелось вникать в этот Gram–Schmidt process, чтобы не вдаваясь в детали попользоваться его результатами. Однако со временем стало ясно что без погружения не получится. Поэтому я отложил в сторону свой 2D Alpha-Beta Filter и решил сделать простое описание процесса Грама — Шмидта как памятку на будущее.

В интернете и литературе математическая сторона дела описана досконально; только ускользает физический смысл: зачем собственно эта ортогонализация нужна. Поэтому я сделал изложение с упором на рассмотрение конкретного примера, причем само изложение идет на трех уровнях: алгебраическом (кому нравится восприятие на абстрактном уровне), на уровне собственно примера с конкретными числовыми данными (для тех кто не любит теорию не подкрепленную практическими задачами) и также на уровне программной реализации. Для последнего я как обычно выбрал Python, который отлично подходит для инженерных задач; при этом можно было ограничиться нотацией питона для записи матричных и векторных уравнений. Тем не менее, формульная запись была сохранена для того чтобы оставить общность рассмотрения.

Сосед с перфоратором

Сформулируем исходную задачу на следующем примере. Мы решили заняться вокалом и записать свое собственное музыкальное произведение. После первых композиций активизируется ваш сосед и включает свой перфоратор, атакуя нашу общую стенку. Будущий сингл века под угрозой!

У вас есть организационно-административное и инженерное решение. Сразу опускаем первый вариант как самый скучный и непосредственно переходим к самому интересному, второму варианту. Очевидно, что можно расположить второй микрофон (а первый вы используете для записи своего голоса) непосредственно у стены и сделать запись шума перфоратора в надежде, что удастся скомпенсировать его в тракте первого, солирующего микрофона.

И эти надежды не беспочвенны. Для того чтобы двигаться дальше, начнем давать обозначения нашей конфигурации. Наша запись, сделанная с солирующего микрофона, подпорченная перфорирующими звуками будет называться X. Это будет вход фильтра, который мы собираемся использовать для подавления шума. Наша конечная цель — убрать из входного сигнала X этот шум подчистую. Другими словами, нам надо знать эту шумовую составляющую D, которая содержится в X, которая в адаптивной фильтрации именуется desired signal.

Здесь я должен вас предостеречь вот от чего. Признайтесь, в вашей голове уже мелькнула шальная мысль взять сигнал с «перфораторного» микрофона и просто вычесть его из записи X. Ну и что, если интенсивность помехи в полезном сигнале и у стенки разные: подкрутим уровень потенциометром, и всего делов. Сразу скажу, что потенциометров понадобится много, в том числе для компенсации сдвига фазы, учета расстояния, перемещения соседа с дрелью за стеной, изменения свойств среды распространения звука по причине допустим заливания соседей сверху… И крутить эти потенциометры придется непрерывно. Собственно, этим и занимается адаптивный фильтр: он непрерывно ищет измеренный сигнал помехи во входном сигнале и старается минимизировать значение ошибки. И если это так, то зачем нам делать за него всю эту работу?

Теперь мы понимаем, что у стены мы записываем шум как некоторую оценку D^ помеховой составляющей D. Эти сигналы связаны, похожи друг на друга, обладают схожими параметрами, но они не идентичны. При этом D^ нам известен в записи как помеха перфоратора у стены, а нашей конечной целью является D. А еще точнее — на самом деле, зная D, мы получим отфильтрованный сигнал X^ = X — D, очищенный от помехи насколько это возможно (в смысле минимума среднеквадратической ошибки, конечно!)

Микрофон включен… поехали

В нашем распоряжении сейчас следующие записи:

$X1 = \begin{bmatrix} -15&35&50&50&25\end{bmatrix}$

будем считать что это нота «ля» нашего вокала, искаженная перфоратором;

$X2 = \begin{bmatrix} -20&30&40&30&-5\end{bmatrix}$

и скажем следующая «подпорченная» нота «си — бемоль».

Алгоритму все равно, каким образом представлены входные сигналы: здесь мы демонстрируем пятимерные векторы. Значок транспонирования, который был бы уместным чтобы не записывать векторы вертикально, для удобства опущен.

Соответственно, сигнал помехи D^ который мы «подслушали» у соседской стенки:

$\hat{D} = \begin{bmatrix} -10&10&0&10&-10\end{bmatrix}$

Теперь подготовим наш главный инструмент — язык Python. Работать будем прямо из командной строки Питона, набирая операторы по мере надобности. Запускаем интерпретатор (у меня в Ubuntu 14.04 стоит python3, а у вас?):

$ python3
Python 3.4.0 (default, Jun 19 2015, 14:20:21) 
[GCC 4.8.2] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>>

$ python3

Python 3.4.0 (default, Jun 19 2015, 14:20:21)

[GCC 4.8.2] on linux

Type "help", "copyright", "credits" or "license" for more information.

>>>

и для начала вводим:

>>> import numpy as np
>>>

1 2	>>> import numpy as np >>>

Команда импортирует модуль numpy, который мы будем интенсивно использовать для работы с векторами и матрицами.

Зададим три наших исходных вектора:

>>> x1 = np.array([-15, 35, 50, 50, 25])
>>> x2 = np.array([-20, 30, 40, 30, -5])
>>> de = np.array([-10, 10, 0, 10, -10])
>>>

>>> x1 = np.array([-15, 35, 50, 50, 25])

>>> x2 = np.array([-20, 30, 40, 30, -5])

>>> de = np.array([-10, 10, 0, 10, -10])

>>>

Векторы в какой — то части заданы совершенно произвольно, я только старался чтобы X1 не слишком сильно отличался от X2 и это различие как-то ассоциировалось с D^.

Замечу, что здесь я не придумал, как обозначить d с крышечкой сверху, и поэтому добавил к d букву e: estimated.

Все, для работы нам больше ничего не нужно. Следующий вопрос, на который надо ответить, будет таким: существует ли строгое теоретическое решение задачи нахождения desired signal D?

Классическое решение…

Строгое теоретическое решение существует, и оно представляет собой одну из форм выражения Винера — Хопфа (это известная тема и ее легко найти в интернете). Вот это соотношение:

$R_{xx} W = P_{dx}$ (1)

Искомым значением является вектор оптимальных весовых коэффициентов W, с помощью которого по входному сигналу будет найдено значение помехи D:

$D = W X$

Rxx представляет собой автокорреляционную функцию сигнала X и для нашего примера будет выглядеть следующим образом:

$R_{xx} = \begin{bmatrix} <X1, \thinspace X1> & <X1, \thinspace X2> \\ <X2, \thinspace X1> & <X2, \thinspace X2> \end{bmatrix}$

где выражение <X1 X2> представляет собой inner product, или dot product, определяемый вот так:

$<X1 \thinspace X2> = \sum\limits_{i=1}^n X1_i \thinspace X2_i$

Попросим Питон посчитать автокоррелационную матрицу для сигналов, которые мы уже ввели в командной строке выше:

>>> rxx = np.zeros((2, 2))
>>> rxx[0, 0] = np.dot(x1, x1)
>>> rxx[0, 1] = np.dot(x1, x2)
>>> rxx[1, 0] = np.dot(x2, x1)
>>> rxx[1, 1] = np.dot(x2, x2)
>>> rxx
array([[ 7075., 4725.],
[ 4725., 3825.]])
>>>

>>> rxx = np.zeros((2, 2))

>>> rxx[0, 0] = np.dot(x1, x1)

>>> rxx[0, 1] = np.dot(x1, x2)

>>> rxx[1, 0] = np.dot(x2, x1)

>>> rxx[1, 1] = np.dot(x2, x2)

>>> rxx

array([[ 7075., 4725.],

[ 4725., 3825.]])

>>>

Запишем автокорреляционную матрицу нашего сольного выступления, подпорченного помехой, выглядит следующим образом:

$R_{xx} = \begin{bmatrix} 7075 & 4725 \\ 4725 & 3825 \end{bmatrix}$

О чем говорит автокорреляция? Значения по главной диагонали 7075 и 3825 фактически представляют собой мощности сигналов X1 и X2 соответственно; по составу этих векторов мы и так видим, что X1 будет помощнее (нота «ля» особенно удалась). Гораздо интереснее значения вне главной диагонали, в нашем случае оно всего одно 4725, и характеризует степень взаимозависимости сигналов X1 и X2. Отметим это в уме и пойдем дальше.

Вектор Pdx показывает взаимную корреляцию между сигналом X и оценочным значением помехи D^:

$P_{dx} = \begin{bmatrix} <\hat{D}, \thinspace X1> \\ <\hat{D}, \thinspace X2> \end{bmatrix}$

Снова обращаемся к Питону:

Python

>>> pdx = np.zeros((2, 1)) >>> pdx[0] = np.dot(x1, de) >>> pdx[1] = np.dot(x2, de) >>> pdx array([[ 750.], [ 850.]]) >>>

1
2
3
4
5
6
7

>>> pdx = np.zeros((2, 1))
>>> pdx[0] = np.dot(x1, de)
>>> pdx[1] = np.dot(x2, de)
>>> pdx
array([[ 750.],
[ 850.]])
>>>

$P_{dx} = \begin{bmatrix} 750 \\ 850 \end{bmatrix}$

Теперь у нас есть все для нахождения вектора весовых коэффициентов из выражения (1).

В недрах модуля numpy Питона есть целый раздел функций для работы с линейной алгеброй, в том числе функция для решения подобных матричных уравнений. Воспользуемся ею и получим W:

>>> w = np.linalg.solve(rxx, pdx)
>>> w
array([[-0.24228029],
 [ 0.52150963]])
>>>

>>> w = np.linalg.solve(rxx, pdx)

>>> w

array([[-0.24228029],

[ 0.52150963]])

>>>

$W = \begin{bmatrix} -0.2 \\ 0.5 \end{bmatrix}$

В результате, находим помеху D, а заодно и наш сигнал, очищенный от помехи:

>>> d = x1 * w[0] + x2 * w[1]
>>> d
array([-6.79598839, 7.16547902, 8.74637107, 3.53127474, -8.66455529])
>>> x1e = x1 - d
>>> x2e = x2 - d
>>> x1e
array([ -8.20401161, 27.83452098, 41.25362893, 46.46872526, 33.66455529])
>>> x2e
array([-13.20401161, 22.83452098, 31.25362893, 26.46872526, 3.66455529])
>>>

>>> d = x1 * w[0] + x2 * w[1]

>>> d

array([-6.79598839, 7.16547902, 8.74637107, 3.53127474, -8.66455529])

>>> x1e = x1 - d

>>> x2e = x2 - d

>>> x1e

array([ -8.20401161, 27.83452098, 41.25362893, 46.46872526, 33.66455529])

>>> x2e

array([-13.20401161, 22.83452098, 31.25362893, 26.46872526, 3.66455529])

>>>

Запишем красиво результат нашей работы, слегка округлив результаты:

$D = \begin{bmatrix} -6.8&7.2&8.7&3.5&-8.7\end{bmatrix}$

$\hat{X}1 = \begin{bmatrix} -8.2&27.8&41.2&46.5&33.7\end{bmatrix}$

$\hat{X}2 = \begin{bmatrix} -13.2&23.8&31.2&26.5&3.7\end{bmatrix}$

Вот собственно и все, поздравляю с успешным решением задачи — наша песня снова звучит, очищенная от назойливого соседского перфоратора. И только один вопрос не дает покоя: при чем здесь собственно ортогонализация Грама — Шмидта?

… которое так и останется на страницах учебников

Если бы этот мир был идеальным, то все было бы просто. Одна строчка np.linalg.solve(a, b) на Питоне, и дело в шляпе. Но поскольку мы еще и инженеры, нас начинает интересовать вопрос производительности. Насколько быстро все это будет работать?

Для оценки быстродействия Питон любезно предлагает нам воспользоваться модулем datetime. Чтобы не создавать исходный сигнал вручную, эксперименты будем проводить над тестовой матрицей размером M, которую мы будем заполнять случайными данными. Делая отметки времени до и после выполнения функции np.linalg.solve(a, b), мы определим время, которое тратится на решение матричного уравнения.

Вот кусок кода, который выводит значение времени для матрицы размерностью в 1000 строк и столбцов:

M = 1000
a = 5 * np.random.random_sample((M, M)) - 5
b = 5 * np.random.random_sample((M, 1)) - 5
n1=dt.datetime.now()
z = np.linalg.solve(a, b)
n2=dt.datetime.now()
print(M, n2-n1)

M = 1000

a = 5 * np.random.random_sample((M, M)) - 5

b = 5 * np.random.random_sample((M, 1)) - 5

n1=dt.datetime.now()

z = np.linalg.solve(a, b)

n2=dt.datetime.now()

print(M, n2-n1)

Результат теста:

1000 0:00:00.119958

1	1000 0:00:00.119958

Результат в 120 миллисекунд наверное неплох. Последовательно наращиваем размер тестовой матрицы с 2000 до 8000 получаем:

2000 0:00:00.816943
4000 0:00:05.747642
6000 0:00:18.522508
8000 0:00:43.691010

2000 0:00:00.816943

4000 0:00:05.747642

6000 0:00:18.522508

8000 0:00:43.691010

Представляете, сколько мне пришлось ждать решения уравнения с 8000 размером тестовой матрицы? Целых 44 секунды. Результат несколько обескураживает, но нас всегда предупреждали, что обращение матриц — это дорогая вычислительная операция.

Не стоит грешить на то, что Питон является скриптовым языком: основная работа идет в Си библиотеках модуля numpy (и есть еще фортрановские библиотеки — не ожидали?), поэтому Питон делает все максимально быстро. У меня обычный комп с тактовой частотой в несколько GHz. Конечно, результат будет лучше, если numpy backend Питона будет работать на числодробилке DSP или Neon (есть и такие реализации). Однако, каким бы не было быстродействие платформы, оно просто убивается увеличением размера выборки.

Хорошо заметно, что вычислительная сложность растет в геометрической прогрессии и это ставит крест на прямом использовании классических теоретических решений.

Ортогонализация как избавление от зависимости

Как существенным образом сократить трудоемкость вычислительного процесса? Все портит автокорреляционная матрица Rxx, в которой учтены все возможные зависимости элементов входного сигнала. Позволим себе немного пофантазировать и представить, что мы работаем с сигналом, для которого автокорреляционная матрица — диагональная, то есть все остальные элементы, не лежащие на главной диагонали, равны нулю. Это говорит о том, что корреляция между элементами сигнала отсутствует, что ведет нас к важному выводу: каждый элемент вектора D может быть оценен только по одному соответствующему элементу вектора X. Это резко сокращает вычислительный объем, который будет линейно зависеть от входной выборки. При этом векторы, описывающий сигнал, будут взаимно ортогональными.

Если опустить промежуточные выкладки, сделанные в предположении что входные сигналы взаимно некоррелированы и сответственно матрица Rxx является диагональной, оптимальные весовые коэффициенты могут быть определены независимо в следующей форме:

$w_i = \displaystyle\frac{<\hat{D}, \thinspace X_i>}{<X_i, \thinspace X_i>}$

Соответственно, найденное решение D будет выглядеть следующим образом:

$D(X_i) = \displaystyle\frac{<\hat{D}, \thinspace X_i>}{<X_i, \thinspace X_i>} X_i$ (2)

Здесь мы плавно подходим к процессу ортогонализации, результат которого примечателен тем, что в нем разрушаются зависимости, в общем случае присутствующие во входном сигнале и автокорреляционная матрица будет представлена как раз в диагональной форме. Однако, этот деструктивный процесс исказит собственно наш полезный сигнал, а это нам надо? С другой стороны, ортогонализация могла бы пригодится только для нахождения весовых коэффициентов, а сигнал уже можно оценить по исходной выборке, которая еще не подверглась ортогонализации.

Все это означает то, что нам нужен ответ на следующий вопрос: возможно ли привести задачу линейного оценивания набора произвольных векторов к задаче оценивания набора взаимно ортогональных векторов и получить идентичные результаты? К счастью, ответ на этот вопрос существует и он — утвердительный. Поэтому мы переходим к манипуляциям с нашими сигнальными векторами X1, X2. Для кого теория это кошмарный сон наяву, следующий параграф можно смело пропустить и продолжать рассмотрение нашего музыкального примера дальше.

Разложение как решение

Здесь наш анализ переходит в геометрическую плоскость, потому что на самом деле векторам, как произвольным так и ортогональным, положено комфортно чувствовать себя в геометрии. Чтобы не ломать голову над пятимерным пространством, рассмотрим пример на обычной плоскости с двумя сигнальными векторами X1, X2. Сейчас мы соединим алгебраическую задачу и ее понятную геометрическую интерпретацию (смотрите рисунок):

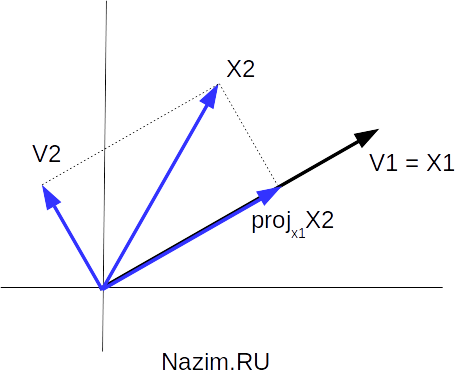
Ортогональное разложение сигнального вектора

Предположим, мы последовательно получили два сигнальных вектора X1, X2. После получения X1, мы выполнили оценку и теперь хотим улучшить ее, пользуясь тем что у нас есть еще и X2. Используя вектор X1 как основу новой, повернутой системы координат, разложим вектор X2 на ортогональные составляющие в этой системе координат. Проще говоря, опустим от конца X2 перпендикуляр на линию на которой лежит X1, и получим проекцию X2 на X1 которую обозначим proj_x1X2. Это будет одна ортогональная составляющая. Вторая составляющая, само собой, будет находится под прямым углом, и ее мы обозначим как V2.

Что касается X1, то будем считать что этот вектор разложен сам на себя и имеет единственную проекцию V1 = X1.

Данный процесс и носит название ортогонализации Грама — Шмидта, когда в результате разложения вектора X2 в системе координат вектора X1 получаем ортогональную пару векторов V1, V2. В общем случае процесс Грама — Шмидта конечно не ограничивается двумя векторами: если мы возьмем третий вектор X3, то он будет раскладываться на векторы X1, X2 и так далее. Если помимо алгебраического и геометрического слегка затронем схемотехнический аспект, то такое последовательное разложение по ортогональным составляющим приведет нас к схеме лестничного фильтра (Lattice Filter), но это уже совсем другая история, которой мы займемся позже.

Очевидно, что если бы не было помех, мы всегда получали одинаковый сигнал и в нашем случае выполнялось бы равенство X2 = X1. Поскольку присутствует помеха, векторы X1 и X2 отличаются по длине и по направлению. При этом геометрически и интуитивно понятно, что V2 является мерой отклонения X2 от X1 и есть не что иное, как величина ошибки.

Не полагаясь на интуицию, попробуем выразить высказанную мысль в математической форме. Из курса линейной алгебры известно, что проекцию одного вектора на другой можно найти следующим способом:

$proj_{x1}(X_2) = \displaystyle\frac{<X_2, \thinspace X_1>}{<X_1, \thinspace X_1>}X_1$

Сравниваем значение проекции proj_x1X2 с выражением (2) которое было приведено ранее, и приходим к выводу, что это не что иное как оценка вектора X2 (который выполняет в этом выражении роль вектора D^) с использованием X1, поэтому мы запишем данное выражение со следующим представлением левой части:

$\hat{X}_2(X_1) = \displaystyle\frac{<X_2, \thinspace X_1>}{<X_1, \thinspace X_1>}X_1$

Далее, из геометрических соображений очевидно что

$X_2=V_2+proj_{x1}(X_2)=V_2+\hat{X}_2(X_1)$

и соответственно если выразить V₂ из правой части то получим

$V_2=X_2-\hat{X}_2(X_1)$

Как следует из этого выражения, V₂ есть не что иное, как разница между вектором и его оценкой, или другими словами — значение ошибки оценивания.

Жизнь в новом базисе

То, что мы сделали в предыдущем параграфе — заменили набор сигнальных векторов X1, X2 на их ортогональных наследников V1, V2. С вектором V1 все ясно:

$V_1=X_1=\begin{bmatrix} -15&35&50&50&25\end{bmatrix}$

Посчитаем что из себя представляет вектор V2:

$V_2=X_2-\displaystyle\frac{<X_2, \thinspace X_1>}{<X_1, \thinspace X_1>}X_1$

где по исходным условиям нашей задачи (нота си-бемоль, не забыли?)

$X2 = \begin{bmatrix} -20&30&40&30&-5\end{bmatrix}$

Вновь призываем Питон, который у нас в консольной строке:

>>> v1 = x1
>>> v2 = x2 - (np.dot(x2, x1) / np.dot(x1, x1))*x1
>>> v1
array([-15, 35, 50, 50, 25])
>>> v2
array([ -9.98233216, 6.6254417 , 6.60777385, -3.39222615, -21.69611307])
>>>

>>> v1 = x1

>>> v2 = x2 - (np.dot(x2, x1) / np.dot(x1, x1))*x1

>>> v1

array([-15, 35, 50, 50, 25])

>>> v2

array([ -9.98233216, 6.6254417 , 6.60777385, -3.39222615, -21.69611307])

>>>

Полученное значение V2:

$V2 = \begin{bmatrix} -10.0&6.6&6.6&-3.4&-21.7\end{bmatrix}$

Пока мы еще не отошли от Питона, проверим ортогональность векторов V1, V2:

>>> np.dot(v1, v2)
5.6843418860808015e-13
>>>

>>> np.dot(v1, v2)

5.6843418860808015e-13

>>>

Не будем слишком придирчивыми и посчитаем число в минус тринадцатой степени за ноль:

$<V_1,V_2>=0$

Это было так, к слову, что-то вроде проверочного упражнения.

Теперь наступает момент истины: до этого, для выражения (2) мы сделали утверждение, что во-первых в новом базисе V1, V2 оценка D будет считаться независимо, а во вторых — ее значение для этого базиса будет таким же, как и для теоретического метода. Проверим это: нам нужен результат выражений

$D(V_1) = \displaystyle\frac{<\hat{D}, \thinspace V_1>}{<V_1, \thinspace V_1>} V_1$

$D(V_2) = \displaystyle\frac{<\hat{D}, \thinspace V_2>}{<V_2, \thinspace V_2>} V_2$

Действительно, первое утверждение справедливо: для нахождения D(V1) используется только V1 и не используется V2, и наоборот (это следствие диагональности новой автокорреляционной матрицы!) Напомню, что исходный вектор D^ выглядит следующим образом:

$\hat{D} = \begin{bmatrix} -10&10&0&10&-10\end{bmatrix}$

Для нахождения значений оценок призываем наш безотказный Питон:

>>> dv1 = (np.dot(d, v1) / np.dot(v1, v1))*v1
>>> dv2 = (np.dot(d, v2) / np.dot(v2, v2))*v2
>>> dv1 + dv2
array([-6.79598839, 7.16547902, 8.74637107, 3.53127474, -8.66455529])
>>>

>>> dv1 = (np.dot(d, v1) / np.dot(v1, v1))*v1

>>> dv2 = (np.dot(d, v2) / np.dot(v2, v2))*v2

>>> dv1 + dv2

array([-6.79598839, 7.16547902, 8.74637107, 3.53127474, -8.66455529])

>>>

Снова красиво округлив результат, получим:

$D(V) = \begin{bmatrix} -6.8&7.2&8.7&3.5&-8.7\end{bmatrix}$

И это точно такое же значение ошибки, полученное теоретическим методом! Теперь у нас есть такой же отфильтрованный сигнал

$\hat{X}1 = \begin{bmatrix} -8.2&27.8&41.2&46.5&33.7\end{bmatrix}$

$\hat{X}2 = \begin{bmatrix} -13.2&23.8&31.2&26.5&3.7\end{bmatrix}$

только сформированный итерационным способом буквально из нескольких арифметических действий.

В результате: оргононализация разрушает корреляционные связи в сигнале, что позволяет представить сложную матричную задачу, которая учитывает все эти связи, в виде отдельных независимых уравнений, решение которых не представляет вычислительной сложности.

Теперь с спокойной душой можно вернуться к 2D alpha — beta фильтру.

ПрОдАвЕц ИгРуШеК

Рубрики

Архивы

Ортогонализация Грама — Шмидта/Gram — Schmidt в адаптивном фильтре

Сосед с перфоратором

Микрофон включен… поехали

Классическое решение…

… которое так и останется на страницах учебников

Ортогонализация как избавление от зависимости

Разложение как решение

Жизнь в новом базисе

Ответить Cancel reply

Last 10 articles

Last comments

Login

ПрОдАвЕц ИгРуШеК

Рубрики

Tags

Архивы

Ортогонализация Грама — Шмидта/Gram — Schmidt в адаптивном фильтре

Сосед с перфоратором

Микрофон включен… поехали

Классическое решение…

… которое так и останется на страницах учебников

Ортогонализация как избавление от зависимости

Разложение как решение

Жизнь в новом базисе

Ответить Cancel reply

Last 10 articles

Last comments

Login